23. Dezember
Thinky braucht noch viel mehr Hilfe, denn bei weitem ist die Bücherei noch nicht fertig eingerichtet -- im Grunde wusste er schon lange, dass das vor Weihnachten nichts werden kann, aber es soll ja auch etwas für die Ewigkeit werden. Zwar steht durch die gemeinsame Arbeit das Gebäude und er hat sich überlegt, wie die Bücher grundsätzlich eingeordnet werden sollen, aber wo genau die Regale stehen werden, ist noch gar nicht festgelegt. Leider kann ihm im Moment auch keiner helfen, da die Wichtel und Elfen mi den kritischen Weihnachtsvorbereitungen beschäftigt sind.
Er zieht also seinen Collageblock hervor und fängt damit an, die Umrisse vom ersten Raum in der dritten Etage aufzumalen: Ein Rechteck mit 9x5 Kästchen und lässt die Tür für den Anfang weg, da diese noch versetzt werden könnte. Daraufhin beginnt er damit, die Regale (2x1 Kästchen) im Raum zu verteilen.
Die Regale für diesen Raum werden nur eine Reihe an Büchern beherbergen, sodass es ausreicht, von einer der langen Seiten an sie heranzukommen (an den Stirnseiten befinden sich die Regalwände). Auch darf gerne eine Regalhälfte komplett verdeckt sein, wodurch das Regal dann aber auch nur halb so viele Bücher beherbergen kann.Wie könnte der Raum eingerichtet werden (ausgehend vom leeren Raum), sodass möglichst viele Bücher erreichbar in den Regalen gelagert werden können?

22. Dezember
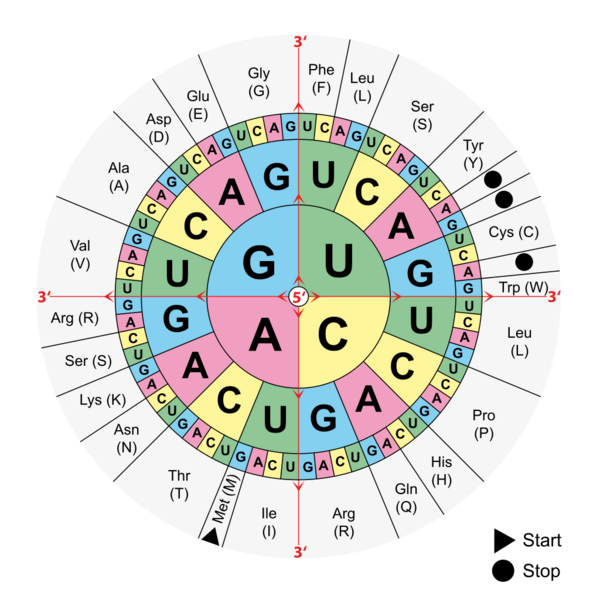
Thinky hat noch nicht beschlossen, wie die Bücherei überhaupt organisiert und eingeräumt werden sollen. Die sonst verbreitete Dewey-Dezimalklassifikation wäre hier nicht sinnvoll anwendbar, da nach kurzer Überlegung eigentlich nur 7 Themen von Belangen sind. Er hat von der weit entfernten Wichtelakademie gehärt, wo damit experimentiert wird, Bücher in Form von DNA zu archivieren. Daran entfernt angelehnt werkelt er an einem System, um Bücher anhand eines DNA-Basen-Codes in der Bücherei zu lokalisieren. So könne das gesamte Gebäude abschnittsweise, etagenweise, regalweise etc. mit den Buchstaben “G”, “A”, “T” und “C” beschriftet werden. Gerade für die Etagen, Regalreihen oder die Position auf dem Regalbrett wären wohl mehrere Buchstaben notwendig...
Würde also ein Buch gesucht werden, könne der Titel in durch die Einbuchstaben‑Abkürzung der Aminosäuren dargestellt und in DNA zurück-übersetzt werden, was dann die Ortsbeschreibung ergibt. Für so richtig praktikabel hält er es nicht, schon weil nichtabgebildete Buchstaben und Sonderzeichen durch Stopp-Codons codiert werden müssen und der Zwischenschritt mit der mRNA alles verkompliziert.
Bitte evaluiere es aber einmal, indem du das Buch aus der Bücherei raussuchst, das durch folgende DNA-Ortsbeschreibung beschrieben wird:
ATCTAATACTGGAGATGTCTCGCATTGCTT
Lösung:
DNA in Triplets aufgeteilt: ATC-TAA-TAC-TGG-AGA-TGT-CTC-GCA-TTG-CTT
DNA in mRNA transkribiert: UAG-AUU-AUG-ACC-UCU-ACA-GAG-CGU-AAC-GAA
mRNA zu Aminosäuren translatiert: •imtsterne -> Zimtsterne
20. Dezember
Heute wird nicht in der Bibliothek geräumt, denn es ist für die Bewohner ein besonderer Tag: es wird der große Baum geschmückt. Und da sie zum Nikolaus je eine Kugel (entweder in Rot, Gold, Silber oder Blau) bekommen haben, wollen sie den Baum mit diesen schmücken. Der feurige Baumschmuck des letzten Jahres hat sie allerdings sehr vorsichtig werden lassen, deswegen erleuchten zwar wieder Feuerbohnen den Baum, doch machen in ausreichender Entfernung in form eines großen Feuers, dessen Licht mit Spiegeln zum Baum umgelenkt wird, um die Kugeln in Scene zu setzen. Da aber noch keine Kugeln hängen, werfen sie nur helle, fast weiße, Kreise an die Stellen, wo später die Kugeln hängen werden. Es wurden bereits in wilder Manier Girlanden aufgehängt und lassen die Schmückenden zum Schluss kommen, dass zwei durch ein Stück Girlande verbundene Kugeln nicht dieselbe Farbe haben sollen. Außerdem sind sie sich einig, dass möglichst wenige Kugel-Farben genutzt werden sollten. Wie könnte der geschmückte Baum aussehen?
Bonus: Einen kleinen Bonus verdienst du dir mit einem ausgeglichenen Baum, der von jeder Farbe mit gleich vielen Kugeln geschmückt ist.
Lösung:

19. Dezember
Als die die Bewohner merkten, dass das Türschloss an diesem Gebäude schwierig zu öffnen war, zerlief sich die Menge bald wieder --schließlich mussten sie auch noch ihren Arbeiten nachgehen-- und so dauerte es zwei Tage, bis sich das Vorhängeschloss vor den wiederversammelten Wichteln und Elfen mit einem KLACK öffnete und sodann auch die großen Türen, die die Sicht auf eine Halle mit Regalen und Büchern freigaben -- Und auf eine mit den Büchern beschäftigte Elfe, die plötzlich aufschaut und an sie herantritt: "Über Jahre habt ihr für Bildung demonstriert und nun gemeinsam eine Bibliothek gebaut, um euer Wissen zu mehren. Zum Glück, aber auch Leider habt ihr auch mehr Grips bewiesen als meine Rätsel abverlangten, denn ich habe es bis jetzt nicht geschafft, sie fertig einzurichten. Mögt ihr mir in der nächsten Zeit dabei helfen? Ohh, ich bin übrigens Thinky, euer neuer Bibliothekar =)
Beginnen wir gleich hier mit dem Regal gegenüber dem Eingang. Es sollte perfekt eingeräumt sein. Also so dass es euch und uns gefällt."
Sie sind sich einig, dass es fünf Bücher zur Geschichte des Dorfes und der Umgebung sein sollen. Doch gibt es da sehr viele passende Bücher zur Auswahl, sodass sie Wünsche nach ästhetischen Maßstäben äußern.
- Damit es schön bunt ist, sollte es ein rotes, goldenes, grünes, blaues und weißes Buch sein.
- Für die Vielfalt muss mindestens ein Buch dünn, mitteldick und dick sein und die Buchrücken einfarbig-schlicht, verziert oder nur mit dem Titel beschriftet.
- Direkt links neben dem Weißen wäre das rote Bich doch sehr passend.
- Ich fände es spannend, wenn das grüne Buch dick und verziert wäre und das Goldene keins von beiden. Oh, außerdem sollen sie die anderen drei Bücher zwischen sich einschließen.
- Mein Wunsch ist klar und kurz: links vom blauen Buch soll ein Schlichtes stehen.
- Auf dicken Büchern ist so viel Platz. Der soll genutzt werden! Da sind schlichte Buchrücken komplett verschenkt.
- Es soll nicht so geordnet aussehen. Deswegen möchte ich nicht, dass zwei dicke oder zwei dünne Bücher nebeneinanderstehen. Aber zu viel Unordnung mag ich auch nicht, deswegen soll auch nicht dick direkt neben dünn stehen.
- Mir ist es wichtig, dass links neben einem beschrifteten Buch immer ein Dickes steht und daneben ein schlichtes.
Welche Bücher haben sie sich ausgesucht?
Lösung:
| gold | blau | rot | weiß | grün |
|---|---|---|---|---|
| schlicht | schlicht | verziert | beschriftet | verziert |
| dünn | mitteldick | dick | mitteldick | dünn |
18. Dezember
In ihrem Kreuzworträtsel in der Sonderedition "Zauberhafte Hanse" hat Wichtelomi Gundi heute eine Frage zur "Weihnachtsstadt des Nordens" beantwortet: "Bekannterweise findet der historische Weihnachtsmarkt neben einer Kirche statt, doch gibt es auch einen in einer Kirche?". Welche ist es?
Lösung: In St. Petri findet einer der Kunsthandwerkermärkte statt
17. Dezember
Wo sich vorgestern noch der schimmernde Schnee auftürmte, steht nun ein ebenso großes Gebäude, das die nach und nach auftauchenden Bewohner in seinen Bann zieht. Die Tür ist verschlossen durch ein großes, sehr seltsames, quadratisches Zahlenschloss mit 81 Einstellrädchen und einigen Markierungen. Auch hängt daran ein Zettel mit nun recht bekannter Schrift: "Wer eintritt in die Hallen des Wissens verlangt, soll seine Würdigkeit ein letztes Mal unter Beweis stellen*". Der schlaue Hellwig hält sich vornehm zurück und lässt die zögerlich herantretenden Wichtel und Elfen gemeinsam rätseln. Würde sich die Tür auch für dich öffnen?
*Genau genommen steht auch noch ein kurzer Text auf dem Zettel, der die Symbole und Markierungen beschreibt, die dieses Sudoku erweitern:
- die drei grauen Balken beinhalten immer die 9 verschiedenen Zahlen in den drei Dreiergruppen "1-2-3", "4-5-6" und "7-8-9" vorwärts oder rückwärts in bel. Reihenfolge ("1-2-3"/"3-2-1" muss nicht die linke Gruppe sein)
- die beiden durch einen goldenen Balken verbundenen Zahlen folgen direkt aufeinander
- liegt eine "1" neben einer "9", ist dazwischen stets ein goldener Kreis gemalt
- die Zahl im goldenen Stern ist nicht größer als "5"
Lösung:

15. Dezember
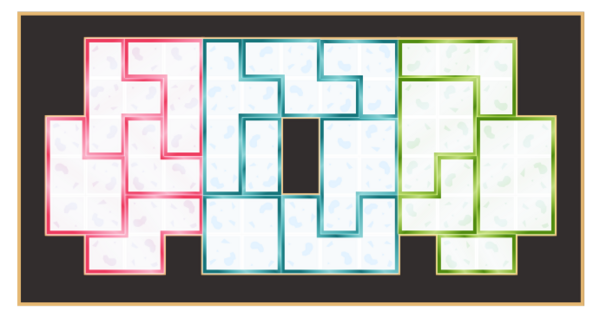
Wieder sollen sie Schnee schippen. Aber dieses Mal soll ein ganz besonderer Turm entstehen. Und es soll auch nicht gewöhnlicher Schnee genutzt werden, sondern dieser wundersame, fast farbig schimmernde Schnee von dort hinten. Doch sie sollen recht hoch bauen und auch die Fläche ist nicht klein. Zudem soll es kein Haufen, werden, sondern eine ausgefallene Form bekommen -- alles sehr mysteriös. Deswegen hat Hellwig die Idee, den Schnee nicht Schäufelchen für Schäufelchen zu transportieren, sondern große Formen zu füllen, zusammenzupressen und so große Bausteine zu formen. Diese sollen dann zum Bestimmungsort gebracht werden und Schicht für Schicht den Turm bilden, bis es hoch genug ist.
Nur wie sollen die Steine zusammengepuzzelt werden? Darüber hat sich Hellwig bisher noch keine Gedanken gemacht. Magst du die Blöcke an ihren richtigen Positionen also bitte im Schichtungsplan einzeichnen? Wichtig ist, dass die linken grünen Bausteine den linken Teil bilden, Die blauen, mittleren das große "O" in der Mitte des Turms bilden und die übrigen grünen Teile den rechten teil des Turms. Außerdem kann pro Schicht nur jeder Baustein einmal genutzt werden.
Lösung:
13. Dezember
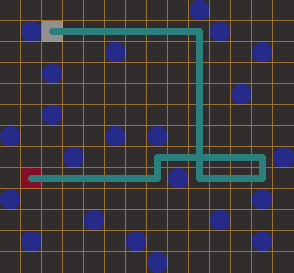
„Sooo viel zu schleppen“, denkt sich die kleine Schleppy. Eigentlich ist die kleine Elfe doch Lageristin, warum soll sie dann wieder so viele Geschenke von hier nach dort bringen? In diesem Fall ist „hier“ das rötliche Quadrat auf der Karte und „dort“ das Graue.
Sie möchte sich die Arbeit heute etwas erleichtern und überlegt, die Kisten mit Zimperschleim einzuschmieren und dann über den vereisten Schnee zu schubsen. So würden die die Kisten gleiten, bis sie gegen etwas treffen, ob Tannen, Schneewehen, schlafende Eisbären oder Trolle, den Schlitten des Weihnachtsmannes oder ihr eigenes Zuhause …
Alle Hindernisse hat sie auf ihrer Karte mit blauen Kreisen markiert. Hilf ihr bitte, den Weg zu planen und gib eine Folge von Himmelsrichtungen (N/O/S/W für oben/rechts/unten/links auf dem Bild) an.Bonus bis Sonntag: Nachdem sie letzte Woche eine spannende arte-Doku über die Geschichte der Achterbahnen gesehen hat, kam ihr noch eine ganz besondere Idee: Sie könnte eine große Rampe bauen und die Geschenke durch die Luft schicken.
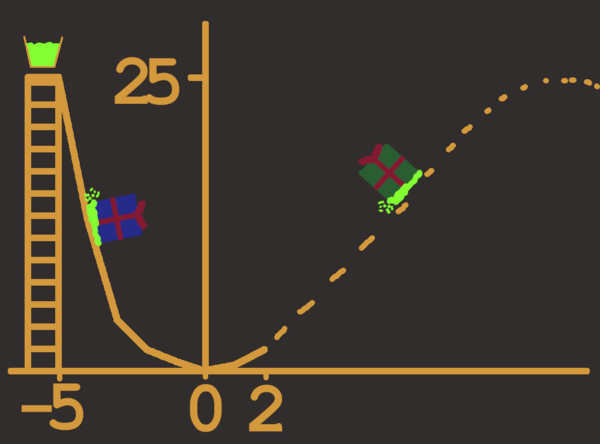
Sie denkt sich, dass eine parabelförmige Rampe (f(x)=x^2) perfekt wäre und wenn sie ganze 25 Meter hoch ist, würden die Geschenke sicherlich sehr weit fliegen. Nach dem Anlauf die Rampe hinab folgt eine sehr kurze Rampe für den Abflug in der Breite von 2 Metern. Danach würden sie in einem parabelbogen weiterfliegen, der sich perfekt dem Ende der Schanze anschließt und ihren Höhepunkt bei ebenfalls 25 Metern haben wird. Warum das funktioniert? Sie wird die Geschenke ebenfalls mit dem Schleim einreiben, was alle Reibung und den Luftwiederstand komplett ignoriert.
Sie hat auch extra eine Skizze ihrer Rampe angefertigt.Was schätzt du, wird es sie glücklich machen? Und wie weit werden die Geschenke fliegen?
Lösung: Es wird die allgemeine Parabelgleichung ($$f(x)=ax^2+bx+c$$) rekonstruiert. Dafür nutzen wir die gegebenen Informationen und bilden vier Gleichungen (Details auf Anfrage) und lösen sie auf. So kommen wir zu $$f(x)=-4/21x^2 + 100/21x - 100/21$$. Die Pakete fliegen damit bis $$f(x) \overset{!}{=}0 => x\approx23.96m$$ Das ist sehr enttäuschend. Sie muss die Geschenke höher tragen als sie fliegen. Das liegt an der schlechten Idee, die Parabel auch als Abflugrampe zu nutzen. Wäre die Rampe allerdings nur 10cm breit, würden die Geschenke theoretisch grob einen halben Kilometer weit fliegen.
12. Dezember
Trotz des stärkenden Kakaos grassiert in einer Wichtelwerkstat die Wichtel-Grippe, denn dort werkeln viele Wichtel zusammen dicht an dicht in einem großen Saal und dekorieren dort die Geschenke. Glücklicherweise zeigen die Wichtel nur schwache Symptome wie eine glühende Nase, hängende Zipfel oder ein raue, tiefe Stimme -- deswegen vermeiden sie das Sprechen, um die Anderen nicht zu erschauern.
Grippeviren, also auch die Wichtelgrippe, haben ein segmentiertes Genom. Das bedeutet, dass die Viren für ihre Verbreitung verschiedene RNA-Segmente in eine Hülle packen müssen. Dadurch kann es zu verschiedenen, neuen Kombinationen kommen, wenn sich ein Wichtel gleichzeitig mit verschiedenen Viren infiziert. In der Werkstatt kursieren im Moment 7 verschiedene Viren-Typen, dessen jeweilige 4 RNA-Segmenten in ihrer Hülle komplett verschieden sind (Ein Virus besteht also aus 4 Segmenten und 2 Viren können sich bei Infektion einer Zelle zu einem neuen Virus rekombinieren. Dabei ergibt sich das erste Segment des neuen Virus aus einem der beiden ersten Segmenten der „Eltern“ usw.).
Zu wie vielen Kombination an neuen Viren kann es in der Theorie kommen, wenn sich die Krankheit ungehindert weiterverbreitet?
Lösung: Nach mehrfachen Rekombinationen kann jedes Segment kann vonem einm der 7 ursprünglichen Viren stammen. Und somit gibt es insgesamt $$7^4=2401$$ Kombinationen. Neu sind demnach $$2394$$ Viren, aber beide Lösungen sind für uns in Ordnung.
11. Dezember
Gerade heute gilt, dass du nicht die perfekte Lösung finden musst, eine deutlich bessere ggf. aber mehr Punkte geben kann.
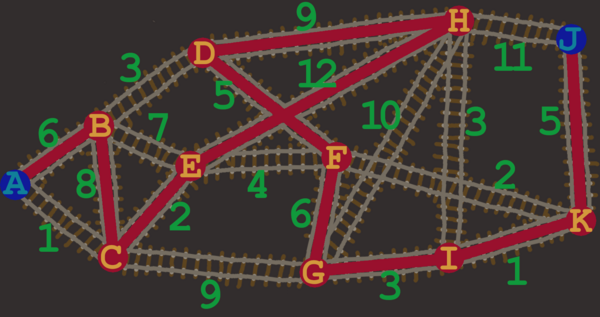
Außerdem ist diese Frage testweise bis um 02:00 beantwortbar.Während der Kakao-Express heute ab 17:30 über die Leinwand im Audimax fährt, bringt er im Norden den arbeitenden wichteln wärmenden Kakao an die verschiednen Arbeitsstätten. Auf der Karte ist ein Ausschnitt des Streckennetzes abgebildet: Die roten Kreise mit den Buchstaben symbolisieren die Weichen, die stets verschiedene Orte iteinander verbinden und an den Strecken dazwischen liegen die Arbeitsstätten. Die grünen Zahlen geben an, wie viele es sind. A und J sind besonders, denn hier befinden sich Bahnhöfe.
Leider ist aktuell das Bahnleitsystem kaputt, weswegen aus Sicherheitsgründen erst alle Weichen gestellt werden müssen und erst dann genau ein Zug durchfahren darf. Das führt leider dazu, dass mit einer Fahrt nicht alle Wichtel ihren verdienten Trunk bekommen. Bitte hilf bei der Planung: Mit welcher Streckenführung können die meisten Arbeitsstätten abgedeckt werden, wenn der Zug von A nach J fährt?
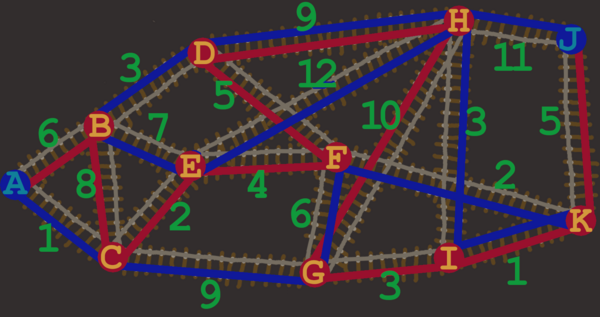
Bonus: Tatsächlich kann der Zug am Zielbahnhof J wenden und von dort auch die Gleise neu gestellt werden. Gibt es nun eine Streckenführung A-J-A, durch die alle Wichtel ihren verdienten Kakao bekommen? Hifreich ist ebenfalls, dass sich bei H eine zweite Weiche befindet, die aber nur vom Bahnhof J gestellt werden kann. Auf der Rückfahrt kann also H sogar zweimal passiert werden, wenn es notwendig ist. Wird eine Strecke auf der Hin&Rückrichtung passiert, macht es die Wichtel doppelt glücklich.
Lösung: 57 und 117 Arbeitsstätten mit folgenden Wegen:
10. Dezember
Die heutige Frage lautet
Sind es riesige Schneeflocken, die vom Himmel fallen? Nein, es sind Flugblätter, die eine große Eule herabgleiten lässt. Und auf der Rückseite unterschireben von… Thinky?
Was steht auf dem Papier geschrieben?
Lösung: Lies in den Hallen des Wissens.

8. Dezember
Heute soll es wieder stark schneien und winden. Das bedeutet, es muss wieder der Schnee im Vorgarten des Weihnachtsmannes geschoben werden. Da sie das letzte Mal so frierten, möchte Blinky einen wärmenden Wichteltrunk zubereiten. Dafür wird sie \(40\%\)igen Marzipan-Likör nehmen und mit einem Gemisch aus zwei Teilen Schneebeerensaft und einem Teil Eisblumenpulver vermengt, bis es nur noch \(2\%\)ig ist -- Für die Wichtel reicht das vollkommen. Unabhängig von der produzierten Menge werden zum Schluss noch zwei Prisen Weihnachtsglitzerpuder hinzugefügt. Wie viel Beerensaft muss sie pressen, um 6Liter des Wichteltrunkes anrühren zu können?
Lösung: Beim Verdünnen haben wir am Ende \(\dfrac{40\%}{2\%}=20\) Mal mehr Flüssigkeit, also wird der Likör mit \(19\) Teilen vom Gemisch gemischt, also: \[6\text{L} \cdot \dfrac{19}{20} = 5.7\text{L}\] Und da zwei Drittel des Gemisches die Beeren ausmachen, wird das folgende Volumen vom Schneebeerensaft gebraucht: \[5.7\text{L} \cdot \dfrac{2}{3} = 3.8\text{L}\]
7. Dezember
Vinky hatte gestern eine blaue Weihnachtsbaumkugel in ihrem Schühchen, hätte aber lieber eine Rote gehab. Ihre Schwester Winky hat von den vier möglichen Farben, die unter allen Wichteln verteilt wurden, tatsächlich auch eine Rote bekommen und würde zur Not auch gerne mit ihr tauschen, doch lag ihre Kugel nicht ganz oben im Stiefel und ist deswegen leider etwas zerkratzt. Wie wahrscheinlich wäre es denn gewesen eine rote, unzerkratzte Kugel zu bekommen, wenn die kleinen Geschenke im Stiefel in zufälliger Reihenfolge übereinander im Stiefelchen liegen und einige Wichtel 5 und genau so viele Wichtel 8 kleinere Gegenstände bekommen haben?
Bonus: Winky möchte ihre Schwester aber überraschen und ihr eine schöne, rote Kugel ertauschen. Wie viele verschiedene Wichtel muss sie dafür fragen, um mit einer Sicherheit von 75% einen Wichtel mit einer Kratzerfreien, roten Kugeln zu finden?
Lösung: \(4.0625\%\), denn dass die Kugel oben liegt, ist im Schnitt $$\dfrac{\dfrac{1}{5} + \dfrac{1}{8}}{2}$$ und da es eine bestimmte von vier Farben sein soll und wir uns Prozent wünschen: $$\dfrac{\left(\dfrac{1}{5} + \dfrac{1}{8}\right)}{2}\dfrac{1}{4}\cdot100 = \dfrac{65}{16} = 4.0625$$.
Bonus: Sei \(R=4.0625\%\) die Wahrscheinlichkeit, eine kratzerfreie, Rote Kugel zu bekommen. "mindestens eine in n Versuchen" bedeutet ja eine oder zwei oder drei oder ... oder \(n\) Kugeln und ist anstrengend zu berechnen. Es ist aber das gleiche wie "nicht keine", was einfach ist, denn keine aus \(n\) ist \((1-R)^n\) und das “eben nicht” ist \(1-(1-R)^n\). Da wir nun eine Wahrscheinlichkeit von mindestens \(75\%\) möchten, folgt: $$1-(1-R)^n >= 0.75$$ Mit etwas Formelgeschubse dann: $$0,25>=0.959375^n$$ und somit schließlich $$33.42 <~ n$$ Somit muss an mindestens \(34\) Türchen geklopft werden.
6. Dezember
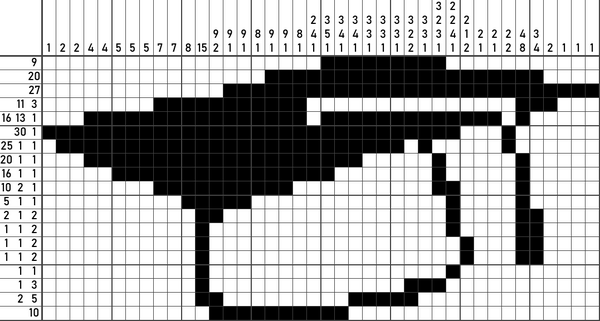
Auch im höchsten Norden wurde gestern je ein Stiefelchen vor die Haustür gestellt und nun am Morgen voller Freude wieder hereingenommen. So sitzen also die Wichtel, Elfen und anderen Bewohner auf bei einer heißen Morgenschokolade ihren Sesselchen und entpacken voller Freude ihren Schuh. Richten wir unseren Blick doch auf die kleine Lageristen Schleppi: Sie zieht eine bunte Tannenbaumkugel, dann einen schokoladenen Troll-Weihnachtsmann (offensichtlich tiefgefroren), einen Mysteriösen Zettel mit Zahlen, ein Fläschchen Zimtschnaps, einige Nüsse und Keks.... Ein Mysteriöser Zettel mit Zahlen? Und dann noch auf der Rückseite eine kurze Anleitung und wieder unterschrieben mit "Thinky".
Was hat das zu bedeuten? Die Anleitung hilft bestimmt: Es ist einfach wie das Lesen: Die Zahl steht dafür, wie viele Kästchen du am Stück in dieser Spalte/Zeile anmalst. Sind es mehrere Zahlen, befindet sich zwischen den angemalten Flächen immer mindestens ein freies Feld.
Lösung:
5. Dezember
Letzte Nacht kam es bei starkem Schneefall zu riesigen Schneewehen. Jetzt ist der Schnee im Vorgarten des Weihnachtsmanns ganz uneben! Die Wichtel sollen nun die enstandenen Schneeberge wieder gleichmäßig verteilen. Der schlaue Wichtel Hellwig hat auch schon die Höhe der Schneetürme ausgemessen und berechnet, auf wie viele Quadratmeter der Schnee verteilt werden muss. Damit der Schnee auch wirklich gleichmäßig verteilt wird, kann er nur auf rechteckige Flächen verteilt werden. Erstelle nun einen Schneeflächenverteilungsplan für die Wichtel.
Lösung:
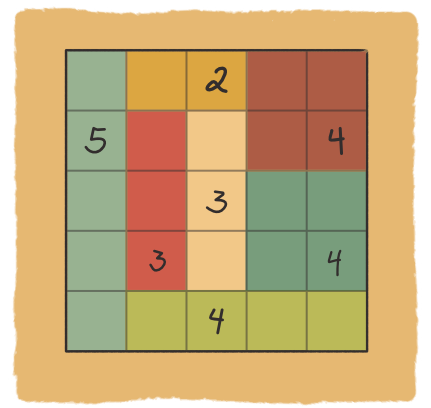
4. Dezember
Heute hatten der Wichtel Blinky und viele andere eine Seltsame Visitenkarte von einem unbekannten Wichtel namens “Thinky” im Briefkasten. Neben dem Namen ist scheinbar nur ein 4x4-Feld aus Buchstaben auf der Karte zu sehen. Hast du eine Idee, was es bedeuten könnte? Zufällig sieht das Feld genau so wie das heutige Snakl auf der Fachschaftsseite der MaIn aus.
Lösung: Wollen Sie Bildung?
| E | I | S | N |
| B | I | L | E |
| D | L | L | O |
| U | N | G | W |
3. Dezember
Zum Adventskränzchen von Vinky und Winky gehört selbstverständlich auch eine Knabberei. Sie wollen für den kommenden Advent Pfefferkuchen backen, sind sich aber beim Rezept noch unsicher. Deshalb fragen sie den backenden Mürbi um Rat, wie viel sie zubereiten sollten und wie viele Zutaten sie überhaupt brauchen werden. Dieser erzählt ihnen von einem geheimen Familienrezept bei dem von jeder der zehn Zutaten nacheinander immer doppelt so viel wie von der vorherigen Zutat dem Teig hinzugefügt wird. Mürbi würde auch gerne die Gewürze für sie mahlen. Bei der Zutatenreihenfolge ist er sich im Moment noch etwas unsicher. Wie viel Gramm Pfeffer müsste er dafür also im schlechtesten Fall für sie zerreiben, wenn die Beiden vorhaben, grob 1Kg Teig für sich und für ihre Nachbarn zuzubereiten?
Tipp: Der Einfachheit halber rechnen die Drei nur mit ganzen Gramm.
Lösung: 1.000? Neunfaches Verdoppeln? Ewas runden? Da kommen einem doch gleich die \(2^{10}=1.024\), bzw. \(2^{10}-1=1.023\) in den Sinn, was der Summe der Zweierpotenzen von \(2^0\) bis \(2^9\) entspricht. Und \(2^9\) ist bekanntlich \(512\).
Das ist aber alles gar nicht so relevant. Denn im Mittelalter wurden unter dem Sammelbegriff “Pfeffer” oft viele exotische (teure) Gewürze zusammengefasst. Somit meint der Name ”Pfefferkuchen", dass im Pfefferkuchen viele Gewürze enthalten sind, doch unser Pfeffer gehört nicht dazu. Folglich muss Mürbi, selbst im schlechtesten Fall, gar kein Pfeffer mahlen.
2. Dezember
Bei ihren Adventskränzchen haben sich Vinky und Winky stets viel zu erzählen. Gerade Winky, die schon viel herumgekommen ist, erzählt viel von Außerhalb. Zuletzt ging es um Lübeck, der anderen "Weihnachtsstadt des Nordens" -- wobei "Stadt" für ihre Heimat ein sehr großes Wort ist. Insbesondere ist Vinky vom Lübecker Weihnachtsmarkt angetan und zählt die vielen Besonderheiten auf, doch hilft das Butterbier nicht dabei, sich genau an den Fakten zu halten.
Wo ist der Wahrheitsgehalt noch am größten?
Lübeck hat den ältesten Weihnachtsmarkt Norddeutschlands — nein, sogar ganz Deutschlands. Nein, sogar ganz Nordeuropas. Okay, zumindest gibt es nördlich von Lübeck keinen älteren Markt — außer unseren natürlich. Außerdem besteht kein Markt der Hanse aus so vielen kleinen, verteilten Teilmärkten wie dieser. Und wusstest du eigentlich, dass der Markt mediale Aufmerksamkeit bekam, aber nicht weil die UNESCO dessen Schönheit als schützenswert eingestuft hat, sondern weil Jumbo Schreiner dort das weltweit größte Marzipanbrot verspeiste? Zudem ist Blinky der zuständige Weihnachtsmarktinspekteur und hat den Markt letztes Jahr mit 8 von 9 Zuckerstangen bewertet.
Lösung: Es ist der älteste Weihnachtsmarkt des Nordens (1648 urkundlich erwähnt), laut der LN sogar der Älteste Deutschlands (wenn alle Älteren wie der Dresdener außer Acht gelassen werden…) – so dachten wir zumidest, denn es stellte sich heraus dass der Stralsunder Markt schon seit 1512 existieren könnte. Damit hat es zumindest einen recht hohen Wahrheitsgehalt.
1. Dezember
Die Adventszeit hat begonnen und Vinky, die kleine Schwester von WInky, brennt schon fast vor Vorfreude. Gestern hat sie zum Adventskränzchen mit WInky um 15:00 die allererste Adventskerze angezündet. Da die Adventszeit ihre Lieblingszeit ist, hat sie schon ein kleines Kerzenlager vorbereitet, schließlich soll eine abgebrannte Kerze sofort ersetzt werden, damit der Kranz bis zum Heiligabend um 20:00 seinen Kerzenschein nie verliert. Die nächste Kerze entzünden die Beiden immer um 15:00 beim gemeinsamen Adventskränzchen mit selbstgebackenen Plätzchen.
Ihre besonders schönen Kerzen brennen übrigens jeweils 6 Stunden und sie hat vorgeplant, dass die Kerzen genau bis zum Heiligabend reichen. Wie viele Kerzen hat sie für dieses Jahr vorsorglich besorgt?
Lösung: \(220\)
Bis zum 24. brennt die erste Adventskerze 24 Tage lang, die Zweite nur noch 17, die Dritte 10 und die vierte Adventskerze 3 Tage. Das sind \(24+17+10+3=54\) Tage pro Adventskerze. Und da eine Kerze nur für 6h hält, werden bis zum 24. um 15:00 genau \(54 \cdot 4=216\) Einzelkerzen gebraucht. Zuletzt fehlen noch \(4\) Kerzen, um die Zeit bis zum Abend zu überbrücken